令和7年度版「新編 新しい数学」
中学校1年
中学校2年
中学校3年
共通
- 0章「算数から数学へ」は、どのような考え方で編集されていますか。
- 算数と数学をつなぐ単元として、また中学校数学の授業開きとしても使えるという意味を込めて「0章」としました。題材は、生徒に馴染みのあるかけ算九九の表で、算数が苦手な生徒でも取り組めます。生徒が見つけたきまりを自由に発表し合う活動を通して、発言しやすい学級づくりにつながります。また、p.4~6の「大切にしたい数学の学び方」も合わせてご指導いただけます。
- 0章で素因数分解を扱った意図を教えてください。
- 新学習指導要領では、「素因数分解」が3年から1年に移行されました。「素因数分解」は、自然数の範囲で考えるため、1章で負の数を学習する前に扱い、生徒に混乱が生じないようにしました。また、素因数分解と同時に、累乗の表し方を扱い、素因数分解の結果を指数を用いて簡潔に表すことのよさを学習します。
- 正負の数の計算方法を、「東西の移動」で説明しているのはなぜですか。
- 計算のしかたの指導にはいろいろな方法がありますが、教科書では、加法、乗法とも「東西の移動」を素材にして指導するようにしています。これは、この素材が次のようなよさを持ち合わせていると考えたからです。
・加法、乗法とも、同じ素材で指導することができ、統一的に扱える。
・生徒にとって身近で具体的な量を背景にしているので、理解されやすい。
・数直線に結びつけやすい。
また、加法では、(移動)+(移動)=(移動)として指導し、加数と被加数を同種のものとして扱っているので、交換法則、結合法則の指導へも無理なく進めることができます。
- 「
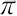 」を、2章「文字と式」で扱っているのはなぜですか。
」を、2章「文字と式」で扱っているのはなぜですか。
- 円周率は小数で表すとかぎりなく続く数ですが、
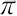 という文字を使って簡潔に表すことができます。このような文字のよさに「文字と式」の学習のなかでふれさせたいと考えています。また、早期に指導することで、その後の学習で使い慣れさせていくことができます。たとえば、1年p.122では、円周の長さが直径に比例することを式で表す際に、比例定数として
という文字を使って簡潔に表すことができます。このような文字のよさに「文字と式」の学習のなかでふれさせたいと考えています。また、早期に指導することで、その後の学習で使い慣れさせていくことができます。たとえば、1年p.122では、円周の長さが直径に比例することを式で表す際に、比例定数として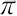 を用いています。
を用いています。
- 4章「比例と反比例」の4節の導入(深い学び)で「行列の待ち時間」を題材にしたのはなぜですか。
- 関数の指導では、具体的な事象における数量の関係をとらえ、それを活用して未知のことがらを予測するなど、関数の考えのよさを理解させることが大切です。「行列の待ち時間」は、生徒にとって身近な場面で必要感があり、関数の考えのよさが理解しやすい題材であると考えました。このような活動を通して数学の有用性を感じさせることをねらっています。
また、「算数・数学の問題・解決過程」をふまえ、「数学化」の過程を重視し、行列が一定に進むと仮定することに気づかせる発問を設けました。「比例とみなす」という考えを使って解決できる場合があることを理解できるようにしています。
- 比例や反比例の表、式、グラフを扱った意図を教えてください。
- 全国学力・学習調査で、関数における表、式、グラフの相互関係の理解が不十分であることをふまえ、1年の比例、反比例から扱い、2年の学習につながるようにしました。比例、反比例のそれぞれの比例定数が、式や表、グラフのどこにあらわれるのかを考える活動を通して、3つの表現の相互関係を理解できるようにしています。
- 5章「平面図形」はどのような考え方で編集されていますか。
- 5章「平面図形」は、1節「図形の移動」→2節「基本の作図」の順に構成しています。「図形の移動」を最初に指導するのは、図形の移動や対称性の見方が、後の作図において活用されるからです。また、基本的な用語・記号は、羅列的に扱うのではなく、図形の移動を学習する過程の必要な場面で取り上げました。これにより、用語・記号の意味や使い方が理解しやすく、定着がはかれると考えています。
- 基本の作図に入る前に、交わる2円の対称性を扱っている意図を教えてください。
- 「交わる2円の対称性」を基本的な作図の根拠にしており、そのことをより明確にするため、2節2項「基本の作図」の冒頭で扱い、作図の学習に生かされるようにしました。
- 6章1節「いろいろな立体」で正多面体を扱っているのはなぜですか。
- 中学校の空間図形の指導においては、念頭操作だけではなく、実際に立体を手にとって考える経験をさせることが大切です。とくに正多面体は、面や辺などの構成要素に着目して考察したり、双対性を見いだしたりするなど、立体図形に対する興味・関心を高める豊富な内容を含んでいます。これらの活動を通して、立体図形に対する見方を豊かにし、以後の学習につなげることをねらっています。
- 「展開図→投影図」の順で扱っている意図を教えてください。
- 展開図は小学校の内容を学び直しながら錐体へとひろげるものであり、一方、投影図は生徒が初めて学習する内容であることから、生徒の取り組みやすさを考慮し、「展開図→投影図」の順に扱っております。
- 立体の求積を「体積→表面積」の順で扱っている意図を教えてください。
- 体積は生徒にとって身近で量的にとらえやすく、小学校の内容を学び直しながら取り組むことができ、計算処理も容易であるためです。なお、球についても「体積→表面積」の指導順に揃えております。
- p.239~240で扱っている題材の意図を教えてください。
- p.225~235ではサッカーチームの1500m走の記録を、p.237~238では体育委員が調査した運動時間を、生徒がデータをヒストグラムに表したり代表値を求めたりして考察を進める流れとしております。
p.239~240では他者が出した結論を、わかっている情報にもとづいて批判的に考察する流れとしております。生徒が日常生活のネット記事や新聞記事などにある他者が導き出した結論を鵜呑みにせずに、自分なりに吟味をして判断できるようになることをねらっています。
- 連立方程式の解の表記を、
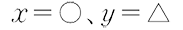 としているのはなぜですか。
としているのはなぜですか。
- 連立方程式の解の表記には、主に以下の3つがあります。
① 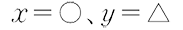
② 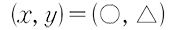
③ 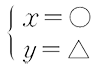
②は解を順序対として、③は解を連立した形として表記しています。弊社の教科書では、解の数学的意味をとらえさせることより、連立方程式が正しく解けることに重点をおき、生徒にとってわかりやすく、書きやすい表記として①を用いています。なお、高校では①の表記が多く用いられています。
また、今回の教科書から、文中の「,」を「、」に変更したことに伴い、①の表記でも「、」を用いています。ただし、数学の表記として変更できない「点の座標」を表す場合は、「(a, b)」のように引き続き「,」を用いることとしています。そのため、「連立方程式の解は2直線の交点の座標を表す」と捉えることもできることから、②の表記では「、」ではなく「,」を用いています。
- 2元1次方程式の表記が
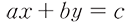 となっている理由を教えてください。
となっている理由を教えてください。
- 2つの2元1次方程式のグラフの交点が、その2つの方程式を連立した解を座標にもつ点であることを学習するため、連立方程式を解くうえで扱いやすい
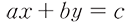 という形で2元1次方程式を示すことにしました。
という形で2元1次方程式を示すことにしました。
- 4章1節「説明のしくみ」は、どのような考え方で編集されていますか。
- 2年の図形の証明の指導においては、平行線の同位角から学習に入っても、生徒にとってはすでに知っているあたり前のことを確認しているようにしか思えず、証明の筋道を追っていくという意味は伝わりにくいと思われます。そこで教科書では、「三角形の内角の和が180゜」であることを既知の性質として認めて出発し、「多角形の内角の和」の性質が、「三角形の内角の和が180゜」であることを根拠にして導かれることに気づかせ、根拠をさぐり、単純な性質をもとにしてより複雑な性質を導いていくという証明の意味や必要感を理解できるようにしています。そして、根拠にした三角形の内角の和の性質を論理的な考え方で確認するために必要な同位角や錯角などの内容を学習する、という構成になっています。
- 三角形の合同条件の表現は、どのような考え方で決めていますか。
- 三角形の合同条件は、以下のように表現しています。
① 3組の辺がそれぞれ等しい
② 2組の辺とその間の角がそれぞれ等しい
③ 1組の辺とその両端の角がそれぞれ等しい
これは「中学校学習指導要領解説 数学編」で記載されている表現に準じたものとしたためです。なお、3年の「相似条件」についても、同様の趣旨で表現を変更しています。
- 7章では、箱ひげ図をどのような考え方で扱っていますか。箱ひげ図の授業で使えるツールはありますか。
- 複数のデータを比較するとき、ヒストグラムや度数折れ線を並べたり重ねたりすることで情報が読み取りづらくなることがあります。そこで、比較しやすいデータの表し方の一例として、箱ひげ図を導入しております。
p.185では箱ひげ図とヒストグラムを比較し、箱ひげ図とヒストグラムのそれぞれのよさを考えることを通して、目的や状況に応じて使い分ける必要があることに気づくことをねらっています。
また、「箱ひげ図」を初めて指導される先生方のために、「Tosho統計ツール」、「四分位数」の求め方や「箱ひげ図」のかき方を効率的にご指導いただける「QRコンテンツ」や「指導用スライド(パワーポイント、Googleスライド)」をご用意しています。
- 3年の章構成は、どのような考え方で編集されていますか。
- 「数と式」の領域は、「1章 多項式」→「2章 平方根」→「3章 2次方程式」の順に構成しています。「平方根」を第2章とした理由の1つは、数学の学習につまずいている生徒にとって、学年の最初は「多項式」のほうが取り組みやすく、最近の生徒の学力の状況をふまえると、その必要性がより強まっている、ということがあります。2つ目の理由としては、「3章 2次方程式」では、平方根の考えをもとにした解法が中心となるため、直前の章を「2章 平方根」としたほうが、学習内容のつながりがよいと考えたからです。
「図形」の領域は、「5章 相似な図形」→「6章 円」→「7章 三平方の定理」の順に構成しています。「三平方の定理」を中学校数学の総まとめと位置づけ、既習の内容と絡めた総合的な問題を扱うようにしています。
- 2次方程式の解法が、「平方根の考えによる解き方」→「解の公式」→「因数分解による解き方」の順序で構成されているのはなぜですか。
- 以前の学習指導要領では、「因数分解による解き方」を主に扱うこととされていましたが、「解の公式」が復活し、扱うことのできる2次方程式が広がりました。そこで、より一般的な解法を主に扱うことが望ましいと考え、「平方根の考えによる解き方」→「解の公式」→「因数分解による解き方」の順に構成しています。なお、これらの解法を総合的に見直す場面として「いろいろな2次方程式」を設け、あたえられた方程式について、どの解法を使えばよいかを考えさせる学習が行えるようにしています。
- 2次方程式の解をx=◎、x=△という表し方にしている理由を教えてください。
- 2つの解が、2次方程式を整理してできる2つの1次方程式それぞれの解であることを明確にするため、x=◎、x=△という表し方にしています。
- 今回の教科書から「、」を使うようになったのはなぜですか。
- 令和4年に文化庁から発表された「公用文作成の考え方(建議)」に則り、「,」を「、」に変更しました。全教科で表記をそろえ、生徒が違和感なく学習できるようにしています。なお、数学の表記として変更できない点の座標を表す場合は、「(a, b)」のように引き続き「,」を用いています。
- QRコードから閲覧できるコンテンツ(QRコンテンツ)の使い方、留意点などがあれば教えてください。
- 各QRコンテンツは、「Dマーク」の記載があるページ右下にある二次元コードからアクセスできます。コンテンツの利用場面の例は各学年の教科書p.2-3、コンテンツの種類に関する詳細は1年p.321、2年p.257、3年p.289に記載していますので、QRコンテンツをご利用の際にご活用ください。なお、これらのQRコンテンツは、検定教科書を採択または購入して使用している場合に、授業や自宅等での個人学習などに利用することができます。
- 問の「ハートマーク」はどのように扱えばよいのですか。
- 「ハートマーク」は、必ず身につけてほしい基本的な問題に付けています。問題の重要度がわかるので、数学が得意でない生徒への指導の目安として役立つとともに、生徒の自律的な学習をサポートします。
- 方程式の文章題において、解答で解の吟味を記述することについてどのような考え方で編集していますか。
- 以前は、2次方程式において解が不適である場合にのみ、そのことを解答に記述していました。しかし、問題解決の過程で、得られた解を事象に戻して解釈することが重視されていることから、1年、2年で解が適している場合でも、吟味を行った上での判断であることを解答で示すようにしています。(1年p.108「これは問題に適している。」、2年p.51「これらは問題に適している。」、3年p.88「~から、x=-2は問題に適していない。x=10は問題に適している。」)
- 「深い学びのページ」はどのような使い方を想定していますか。
- 「深い学びのページ」では、問題発見・解決の過程を重視した数学的活動が行えるようにしています。ほぼ全ての章に位置づけています。側注の「問題をつかむ→見通しをたてる→問題を解決する→ふり返る→深める」の過程に沿って、生徒が自ら考え、対話を通して深め授業を展開していただきたいと考えております。
なお、教師用指導書の資料編には、全ての「深い学びのページ」の指導案、ワークシート例、板書例をご用意しておりますのでご活用ください。
- 「クイックチェック」はどのようなコーナーですか。
- 従来の教科書では、学習した内容を確認する問題として、節末に基本の問題、章末に章の問題を設けていました。今回の教科書では、これらに加え、さらに細かな単位で学習した内容の確認を行える問題として「クイックチェック」を新設しました。問題の難易度は、問のハートマークの問題と同程度です。また、クイックチェックにはQRコンテンツ「ヒントと解答」が付いているので、生徒が自分でヒントや解答を確認することができます。クイックチェックは、授業時数配当外ですので、必要に応じてご活用ください。
- 「ちょっと確認」はどのような使い方を想定していますか。
- 「ちょっと確認」では、小学校や前学年などの既習内容のうち、定着率が思わしくないものを中心に取り上げています。例などの指導にあたって、既習内容の確認が必要と思われる場合に授業の中で取り上げたり、生徒の個に応じて取り組ませたりすることができます。また、「ちょっと確認」にページが書かれているものは、当該学年の関連箇所を示しており、「算数」と書かれているものは、小学校の既習内容を示しています。
なお、巻末折込の「学びのつながり」では、小学校の既習内容(1年)や前学年の既習内容(2・3年)をまとめて示していますので、必要に応じて扱うこともできます。
- 「補充の問題」はどのような使い方を想定していますか。
- 「補充の問題」は、「問」の類題として巻末に示しています。「問」にリンクを示してあり、授業中に「問」を終えた生徒が自ら進んで取り組めるようになっています。また、★マークがついた問題は、問で扱っていない型や工夫して解く問題などを取り上げているため、生徒の個人差に対応しやすくなっています。また、補充の問題には、解答や本文の問に戻るリンクも示してあり、家庭学習などの自学自習にもお使いいただけます。
- 「巻末のページ」はどのような使い方を想定していますか。
- 巻末には「数学の目でふり返ろう」「学びのベース、学びのマップ」「補充の問題」「数学の自由研究」があり、いずれも時間配当外の内容で、生徒が主体的に取り組むものとして位置づけています。
「数学の目でふり返ろう」では、その学年の学習で働かせた見方・考え方を、これまでの学習と関連付けて振り返ったり、条件を変えてこれからの学習を想起したりすることを通して、見方・考え方のよさを実感できるようにしています。同様に3年の「学びのマップ」でも、3年間で学習した内容を関連付けて振り返ることができるようにしています。
「学びのベース」「補充の問題」では、前の学年の復習をしたり問の反復練習をしたりすることができます。また、「補充の問題」では少し難易度が高い問題に★印が付いているため、数学が得意な生徒が難しい問題に挑戦することもできるようになっています。
「数学の自由研究」では数学の学習だけでなく、日常生活や他教科の学習と関連した課題に取り組めるようにしています。また、課題に取り組んだ成果を発表し思考力・表現力を高められるように、レポートのまとめ方やスライドのつくり方の例も紹介しています。
- 巻頭の「数学マイノート」で、ノート指導に関わる内容を取り上げたのはなぜですか。
- 学習指導要領では、言語活動の充実をはかることが求められており、その一環としてノート指導に関する内容を取り上げました。
巻頭の「数学マイノート」のように、自分の考えだけでなく、他者の考えや気づいたことを書きとめたり、それをふり返って見直したりすることは、授業や問題解決の流れがわかりやすくなるだけではなく、数学的な思考力、表現力の育成にもつながります。
なお、本文中の「例」の解答はノート形式で示しています。そこでは、分数を2行にわたって書く例や、「=」を揃えて書く例など、解答を記述する際に心がけることにもふれています。
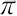 」を、2章「文字と式」で扱っているのはなぜですか。
」を、2章「文字と式」で扱っているのはなぜですか。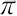 という文字を使って簡潔に表すことができます。このような文字のよさに「文字と式」の学習のなかでふれさせたいと考えています。また、早期に指導することで、その後の学習で使い慣れさせていくことができます。たとえば、1年p.122では、円周の長さが直径に比例することを式で表す際に、比例定数として
という文字を使って簡潔に表すことができます。このような文字のよさに「文字と式」の学習のなかでふれさせたいと考えています。また、早期に指導することで、その後の学習で使い慣れさせていくことができます。たとえば、1年p.122では、円周の長さが直径に比例することを式で表す際に、比例定数として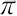 を用いています。
を用いています。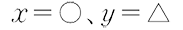 としているのはなぜですか。
としているのはなぜですか。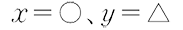
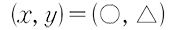
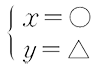
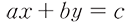 となっている理由を教えてください。
となっている理由を教えてください。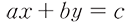 という形で2元1次方程式を示すことにしました。
という形で2元1次方程式を示すことにしました。
