小学校 算数
小学校「新編 新しい算数」
- うさぎを数える際の助数詞は「羽（わ）」か、「匹（ひき）」かについて
- 「１人」と表記していることについて
- 「数」の読み方について
- 演算記号、符号、％、分数、わり算の筆算の書き順について
- 帯分数表記、仮分数表記について
- 1年算数ブロックの縦、横の方向について
- 1年①の判型について
- 1年 入門期の算数ブロックによる6～10の表現について
- 1年 数の合成・分解について
- 1年100までの数表で「0」から始めていることについて
- L（リットル）などの単位記号の表記について
- 2年 筆算と暗算の指導順序について
- 2年テープ図や線分図における、全体と部分の表し方について
- 2年九九の唱え方について
- 2年、3年筆算で繰り上がりや繰り下がりの補助数字を書く位置について
- 3年あまりのあるわり算の「あまり」を「･･･」と書くことについて
- 筆算における小数点の処理について
- 3年「三角形と角」の導入教材を、ストローではなく円周上の点を結んだ三角形づくりにしていること
- 4年 兆よりも大きい数「(し)」の漢字
- 4年「わり算の筆算（２）」と「概数」の指導順序
- 4年「がい数の表し方と使い方」における「約」の用い方
- 概数の表し方の表現「上から」の読み方
- 5年「四角形と三角形の面積」で平行四辺形から導入していること
- 教科書ではうさぎを数える際の助数詞として「匹（ひき）」が使われていますが、うさぎの助数詞は「羽（わ）」が正しいのではないでしょうか。
- NHK出版発行の『ＮＨＫことばのハンドブック第2版』によりますと、動物の数え方の基準として、うさぎを含む動物一般には「匹（ひき）」を、鳥類には「羽（わ）」を用いることとされています。 また、小学館発行の『数え方の辞典』によりますと、うさぎは慣習的に「羽（わ）」で数えるが、動物として数える際は「匹（ひき）」が適当であるとされています。
上記の基準から、教科書におけるうさぎの助数詞としては、「匹（ひき）」を用いることが適切であると考えます。さらに、上記の基準に照らして考えますと、「羽（わ）」は鳥類に用いる助数詞ですので、鳥類ではないうさぎを「羽（わ）」で数えることは助数詞の例外的な使い方となります。教科書で、うさぎを数える際に「羽（わ）」という助数詞を取り入れますと、児童は、算数の問題に取り組みながら、同時に例外的な助数詞の使用にも配慮する必要が生じてしまいます。児童の発達段階によっては、うさぎを「羽（わ）」で数えることにより負担が大きくなり、学習の際に混乱を招くことも考えられます。
これらのことを踏まえまして、教科書では、うさぎの助数詞は「羽（わ）」ではなく「匹（ひき）」を用いています。 - 教科書では、「ひとり」という語の表記として、算用数字の「１人」が使われています。「ひとり」という読み方は、漢数字で「一人」と表記した場合にのみ認められているものなので、「１人」と書くのは間違いではないでしょうか。
- 「新しい算数」では、算数の学習において数に着目させるという意図から、数字は原則として算用数字を用いて表記しています。また、助数詞については、発達段階に配慮しながら慎重に用いるようにしています。
「人」という助数詞は、低学年では最も身近な日常場面で用いられ、「ひとり分はいくつ」「ひとりに何個ずつ分ける」などという算数の学習内容にも関わることが大変多く、紙面上では必要不可欠な語です。
「人」という助数詞を使う場合に、「ひとり」「ふたり」を、漢数字を用いて「一人」「二人」と正しく表記すると、３以上の数値（「３人」「４人」など）と表記の不統一が生じることになります。また、「ひとり」「ふたり」と平仮名で表記すると、数に着目しにくくなり、算数の学習に支障が生じる恐れがあります。
これらのことを踏まえまして、数に着目させるという算数科指導のねらいに基づき、また、表記の統一を図るために、算用数字を用いた「１人」「２人」という表記を採用しています。
「１人」「２人」を「ひとり」「ふたり」と読むことは、正しくは認められていませんが、慣用的に広く用いられ通用している表現と認識しています。また、「１人」「２人」という表記に対して他の読み方をあてることもできませんので、「ひとり」「ふたり」と読むこととする、というのが私どもの考えです。 - 「数」の読み方について、2学年の教科書では「かず」と振り仮名を付けていますが、「すう」と読んでもよいでしょうか。
- 教科書に出てくる「数」の読み方について、「数」は２学年の配当漢字であるため、２学年では振り仮名を付け、その振り仮名は「かず」としています。一方、３学年以上では特に振り仮名を付けておらず、また、教科書紙面で「すう」と読ませている箇所はありません。
しかし、これらを「すう」と読んでも差し支えはないと考えます。「整数」を「せいすう」と読むように、熟語であれば「すう」ですが、一文字の「数」は人によって「かず」と読んだり「すう」と読んだりといずれの読み方も慣用されていると考えます。 - ・教科書では演算記号や等号、分数の書き順が示してありますが、それには何か基準がありますか。また、違う書き順で書いてもよいでしょうか。
・わり算の筆算では、被除数、除数、筆算の記号はどのような順序で書くのが正しいか教えてください。 - 以前は「確かでないことは教科書には載せない」との立場から、演算記号や分数の筆順など、明確な筆順が存在しないものについては教科書には載せておりませんでした。しかし、「児童に好きな筆順で書いてよいと指導すると、混乱が生じることもあるので、正式な筆順がないとしても、何らかの筆順を示して欲しい」との要望も多く、現在の教科書では、「＋、－、×、÷」などの演算記号や等号、「％」の記号、分数などについても筆順を示すようにしています。また、わり算の筆算については、教科書ではなく、教師用指導書に筆順を掲載しています。
以下に、「演算記号や等号、パーセント記号」「分数」「わり算の筆算」について、教科書または指導書で示している筆順について説明します。
ただし、以下に示されている筆順は、あくまで筆順がわからないことによる児童の混乱を防ぐためのものであり、単なる一例にすぎません。必ずこの通りに書かねばならないというものでも、そのように指導しなくてはならないというものでもありません。
（１）演算記号（＋、－、×、÷）や等号（＝）、パーセント記号（％）について
これらの記号について明確な筆順は存在しないようです。また、これらの記号の由来（※例「％」）から、筆順を判断する手がかりが得られないかと考え、文献等を調べましたが、やはり確たる根拠は見当たりませんでした。
そこで、筆順を掲載するにあたり、私どもでは「一般的によく行われる筆順であること」と「小学生にとって書きやすく、自然に受け入れやすい筆順であること」の２点を考慮し、現在掲載している筆順を採用いたしました。
※註「％記号の由来」
「per cent」という言葉は15世紀にヨーロッパの商業の中心であったイタリアで多く用いられるようになり、当初は「ｐ cent」 などと表記されていました。その後、「ｐ」が省略され、「cent」が「Ｃの真上に小さい・を付した記号」に変わるなど徐々に変化を続けた結果、最終的に現在の「％」になったとのことです。
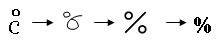
もともとイタリアではprimo（第１）、secundo（第２）･･･などの代わりに、１や２などの数字の真上に小さい・を付した記号で表す習慣がありました。そのため「100について１」という共通単位を表す際に、cent（100）の頭文字をとって「Ｃの真上に小さい・を付した記号」が使われるようになったようです。
（参考文献）
「数字と数学記号の歴史：大矢真一、片野善一郎 著」(1978、裳書房)
「算数・数学授業を楽しくする数学史の話：上垣渉 著」(1990、明治図書）
（２）分数について
分数の筆順の掲載にあたり、私どもでは、「前後の数や記号などとのバランスを崩さずに書けること」に主眼を置き、下記[１]～[３]の３案について検討いたしました。
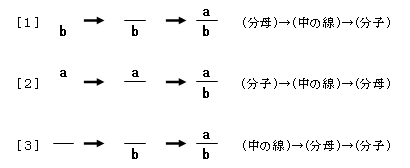
[１]の書き方は「ｂ分のa」という分数の読みに対応したものであり、こちらの方がよいのではないか、とも考えました。しかし、分数表記に不慣れな段階で[１]や[２]の筆順で書くと、これまでの数や式の表現の経験から、下のように前後の数や記号と同じ高さに、同じ大きさで分母や分子を書いてしまう恐れがあります。
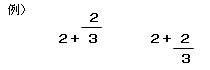
これらの表記は、前後の数や記号とのバランスが悪く読みづらいことに加え、「（２＋３）が分母なのか」、「（２＋２）が分子なのか」といった混乱を生じさせることにもつながります。
以上のことから、中の線を最初に書く[３]の筆順であれば、[１]や[２]と比べて前後の数や記号などとのバランスを考えやすく、かつ誤解も生じにくいと考え、[３]の筆順を示すことにしました。
（３）わり算の筆算について
わり算の筆算については、「筆順に関して児童が戸惑うことが少ない」という意見が多く、現在弊社の教科書には筆順は載せていません。しかし、「指導上の工夫として児童に対する目安が欲しい」という要望もありますので、指導書では下記の筆順を紹介しています。
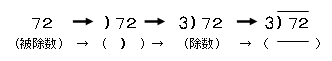
これは、わり算を声に出して読んだときの順番に対応させようという指導が背景にあります。つまり、上記の筆算を声に出して読むと「７２わる３は」となりますが、７２と３の間の「)」を「わる」に、７２の上の「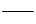
」を「は」に対応させることで、式を読む順番通りに筆算が書けるように、との配慮からです。
なお、他に、
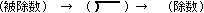
という筆順も紹介しています。
繰り返しになりますが、上記に紹介いたしました筆順のいずれも、正式なルールではありませんので、学級や児童の実態に応じて柔軟な取り扱いをすることが肝要かと考えます。 - 教科書における分数の計算の答えの表記で、帯分数（仮分数）の場合と、仮分数（帯分数）の場合とがありますが、使い分けのルールはどのようなものでしょうか。
- 分数の四則計算において、計算結果が１より大きくなり、答えを分数で表現する場合に、帯分数もしくは仮分数を用いることが考えられます。
数学的には、どちらで表現しても問題ありません。その上で、「新しい算数」では以下のような表記の原則を定めています。
例えば、
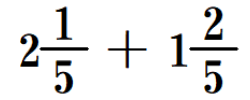
と
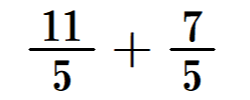
を比較してみます。答えの大きさは同じですが、前者は、問題に帯分数を用いていることから、被加数、加数の大きさを捉えやすく表現した上で計算し、したがって和も大きさを捉えやすく表したいという意図があると想定し、答えは帯分数を優先して
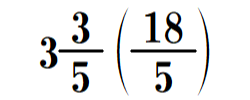
と表記しています。後者については、問題に仮分数を用いていることから、代数的に和が求められれば計算の目的は達成されると想定し、答えは仮分数を優先して
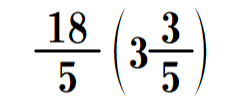
と表記しています。
繰り返しになりますが、数学的には大きさが等しいため、帯分数、仮分数のどちらで表しても問題はありません。 - 1年の教科書では、算数ブロックが縦並びになっている場合と、横並びになっている場合がありますが、どのような意図があるのですか。
- 1年の教科書では、ブロックの置き方について、「数の構成を学習する場面では縦置き」「計算など操作を中心とした場面では横置き」にしています。その理由としては、前者は位取りの考えにつなげる上で、縦置きで示した方が記数法との関係で対応がとらえやすいことが挙げられます。また、後者は、児童の操作において、身体的な位置の関係から横置きの方が操作しやすいということを考慮しております。
例えば、1年②38～39ページでは、「10と3で13」というような数の構成を学習しますので、ブロックを縦置きで示しています。また、1年②44～45ページでは、10＋5や15－5のような計算を学習しますが、ここでは、「15は10と5」というような数構成をもとに加法や減法の式に表すことで、数構成の理解を深めることをねらいとしておりますので、縦置きのブロックで示しています。一方で、第9単元「3つのかずのけいさん」や第11単元「たしざん」、第13単元「ひきざん」では、ブロック操作をしながら、3つの数の計算や、繰り上がり・繰り下がりのある計算の仕方を考える場面ですので、ブロックを横置きにして、ブロックをたしたり、ひいたりする操作を示しています。
なお、ブロックの置き方や操作の仕方には、明確な決まりはなく、教科書で示しているものはあくまで例示になります。実際の授業では、学級の実態などによって、各先生のご裁量にて柔軟にご判断いただければと考えます。 - １年①は、なぜA４判なのですか。
- 入門期の学習のしやすさを追求した結果、A４判にしております。
具体的には
①算数ブロックを紙面の要素と対応させやすい（紙面が広く、ブロックを対応させる要素と要素の間の距離を十分に確保できる）
②市販のノートを使用するのと同じように教科書に書き込むスペースを確保できる（ノート機能をもたせたオールインワンの構成とすることにより、授業中の教科書、ノートの出し入れが不要で、算数の学習に集中しやすい）
などのメリットがあります。
また、これらのメリットがさらに際立つように、より開きやすくフラットになりやすい製本方式を採用したり、鉛筆で書き込みやすく消しやすい専用の紙を使用したりもしています。 - 6～10の学習等で、算数ブロックを一列に並べるのにはどのような意図があるのですか。
- 結論から申し述べますと、後の十進位取り記数法に基づく数の表現や計算の学習を進めるにあたっては、10で１こととらえることが必要となり、その素地をしっかりと培うためです。
入門期においては、「５といくつ」と数をとらえることも大切にし、右のような数図も合わせて掲載しています。
また、算数ブロックは、10までを一列に並べることを原則としていますが、５といくつといったとらえ方のほうが数をとらえやすい児童にも配慮し、５と５の間を空けたり、５と５の境目に罫線を入れたりしています。
さらに、その後の加減法の学習などでは、10の補数のとらえやすさにも配慮し，下側にケースをつけた図を使用するなどしています。
繰り返しになりますが、十進位取り記数法に基づく数の表現や計算の学習を進めるにあたっては、10のまとまりを１こととらえることが必要となります。５といくつ、というように並べると数をとらえやすいという面があることも承知していますが、５といくつという並べ方を継続すると、常に「５といくつ」といったように数をとらえる習慣が身についてしまい、10のまとまりを１こととらえることが困難になるという弊害があることに配慮した取り扱いとしています。 - １年①の数の学習における、合成・分解の取り扱いにはどのような意図があるのでしょうか。
- 学習指導要領では、これまでも「新しい算数」が大切にしてきた「深い学び」や、主体的に学習に取り組む態度の育成がますます重視されています。これらのことを踏まえると、１つの数の読み方、書き方について知ったならば、その数について合成・分解という視点でより深く理解するという学習がたいへん重要であると考えます。
例えば、５の読み方、書き方について学習したら、さらに５を合成・分解の視点からより深く理解できるようにしています（１年①p.12～13）。そして、次に６以降の数を学習する際には、その数の読み方、書き方を知るとともに、５の学習と同じように合成・分解の視点から数についてより深く調べる、また、調べてみたいといった深く学ぼうとする態度を育成することも大切です。
以上のことから、
・ある数の読み方、書き方を学習したら、合成・分解の視点からその数をとらえ、より深く学ぶことができるようにする。また、より深く学ぼうとする態度を養う（１年①p.12～29）。
・その上で、順序数まで学習した後、関数の考えの素地を織り交ぜつつ、あらためて数を合成・分解の視点からとらえる（１年①p.38～40）。
という段階的かつ重層的な学習段階を設定することとし、数に対する感覚を育てるとともに、加減計算の素地を培うことを意図しています。また、より深く学ぼうとする態度を育成することもめざしています。
すなわち、数の合成・分解の取り扱いについては、従来のような「いくつといくつ」という単元の設定こそしていませんが、いっそう充実させています。 - 1年の100までの数表で、「1」からではなく、「0」から始まっているのはなぜですか。
- 1年の100までの数表(1年②99ページ)で「0」から始めている理由は大きく分けて2つあります。
まず、十進位取り記数法の理解の定着をねらっていることが挙げられます。第14単元「おおきいかず」以前の単元では、数えることを中心に扱ってきましたが、この単元では、初めて位取りの考えを導入します。目標として「十進位取り記数法のよさに気づくこと」を掲げており、「一のくらい」「十のくらい」という用語を学習します。「0」から始まる数表では、「20、21、22、･･･、29」と十の位の数字が同じ数が横一列に10個並んでおり、例えば20台の数が10集まると次は十の位の数が1増えた30台の数になる、ということが見やすくなっています。すなわち、「9と10の間、19と20の間、29と30の間、･･･」でそれぞれ改行することで、十の位が同じ数である10個の数のまとまりを意識させることをねらいとしています。
また、数表を数直線と関連づけて扱うことも意図しています。教科書でも数直線を示していますが、数直線では最初の目盛り（基点）は「0」になっています。数表でも｢0｣を示すことで、数直線と対応させやすくなると考えます。数表を数直線と関連づけて扱うことで、数表で示した100までの数を集合数としてだけでなく、順序数としてもとらえられるようにするというねらいがあります。 - 「リットル」の表記を「Ｌ」にするなど、単位記号の表記に対する考え方を教えてください。
- 平成23年度用教科書から「リットル」の表記を「ℓ」から「Ｌ」に、「デシリットル」を「dＬ」にするなど、単位記号の表記を変更しました。これらの表記の変更は、「単位記号の表記は、国際単位系に定められている表記基準にあわせる」という文部科学省からの検定意見によるものです。この変更は、算数科だけでなく、社会、理科、家庭科など全教科が対象となりました。
国際単位系では、「単位記号は立体で表記する」と定められています。弊社の教科書では平成17年度用まで、「斜体」（斜めに傾いている書体）で表していましたが、平成23年度用から新たに立体の書体を検討、開発し、すべての単位記号の表記を「立体」（直立している書体）に変更しました。
「リットル」につきましては、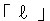
のように、これまでの筆記体を直立させたような字形の書体も許容の範囲内ではあるものの、国際単位系の表記として正式に使用された例はないようです。従いまして、小文字の「ｌ」か大文字の「Ｌ」で表記することとなりますが、小文字の「ｌ（エル）」は数字の「１（いち）」と間違えやすいことから、大文字の「Ｌ」の使用が国際単位系で推奨されています（※）。このようなことを踏まえまして、「リットル」は大文字の「Ｌ」で表記することとし、これらの表記が文部科学省の検定で認められました。
なお、「g」（グラム）や「a」（アール）は、一般的な立体の字形は小学生では書きにくいこと、「t」（トンの立体の字形は他の文字と混同する恐れがあることなどの理由から、それぞれ筆記体の字体を直立させたような字形の書体にしました。
※参考
・独立行政法人 産業技術総合研究所 計量標準総合センターのホームページ
「国際単位系（ＳＩ）は世界共通のルールです」パンフレット - 2年で、筆算を暗算より先に指導しているのはなぜですか。
- 「新しい算数」では、筆算を先に学習し、その後に暗算を学習する配列としています。
これには、いくつかの理由があります。
まず、計算に苦手意識がある児童も、数によらず同じ方法で答えを求められる筆算を習得することで、安心感をもって学習に取り組むことができます。
また、筆算の学習を通して数の構成に対する理解を深め、数に対する感覚を磨いた後に、 適切なタイミングで暗算を学習することで過度な負担感がなくなり、結果として暗算を必要に応じて適宜活用できるようになると考えられます。
さらに、数によらず同じ仕方で計算できるというアルゴリズムのよさを実感する学習は、数学のよさを実感する絶好の機会です。以後の学習においても、乗法や除法で同じように効率的・効果的に計算する方法はないかと発展的に考える数学的な見方・考え方を働かせ、成長させるためにも、発達段階に配慮しつつ、印象に残りやすい早期に実感すべきであると考えます。
なお、「小学校学習指導要領（平成29年告示）解説 算数編」p.109の23行目以降の内容から、第2学年の加法、減法の学習の中心は、2位数の加法及びその逆の減法計算とそれらの筆算の仕方についての理解であると解釈できることも、筆算を最初に扱っている理由の１つです。
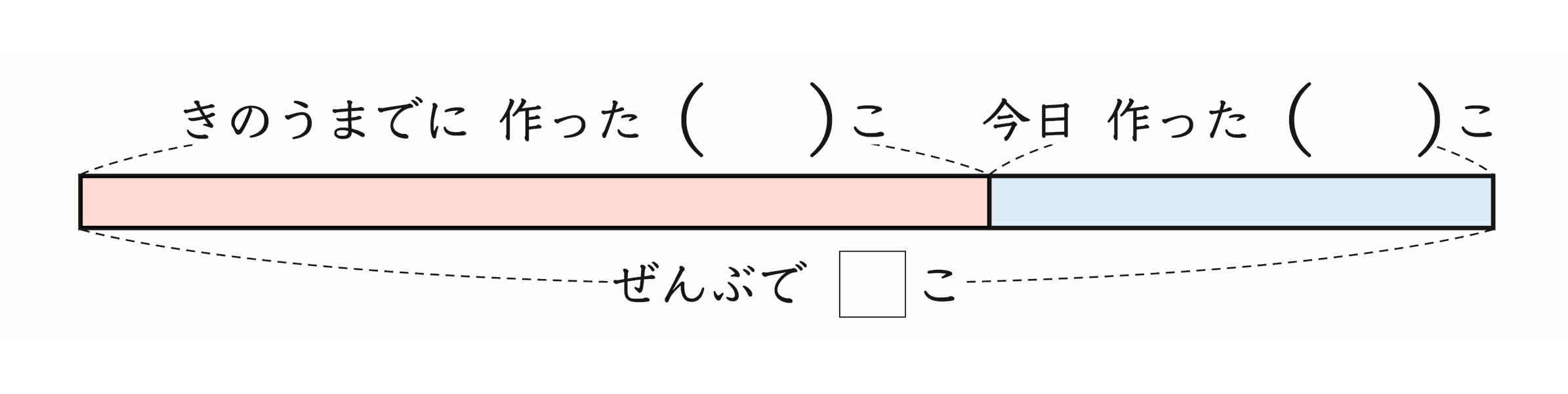
暗算は、児童によって得意、不得意が別れやすい面がありますので、数の学習と密接に関連づけながら、取り扱いに際しては個に応じた配慮と工夫が不可欠であると考えます。 - 2年上巻87ページ問題１の図では、テープ図の上部が部分（「きのうまでに作った数」「今日作った数」）、下部が全体（「ぜんぶの数」）となっています。一方、2年下巻72ページ枠内の図では、テープ図の上部が全体（「ぜんぶの数」）、下部が部分（「赤の数」「青の数」）となっています。図で全体と部分の表し方には、何かきまりがあるのでしょうか。
◆2年上87ページ
◆2年下72ページ
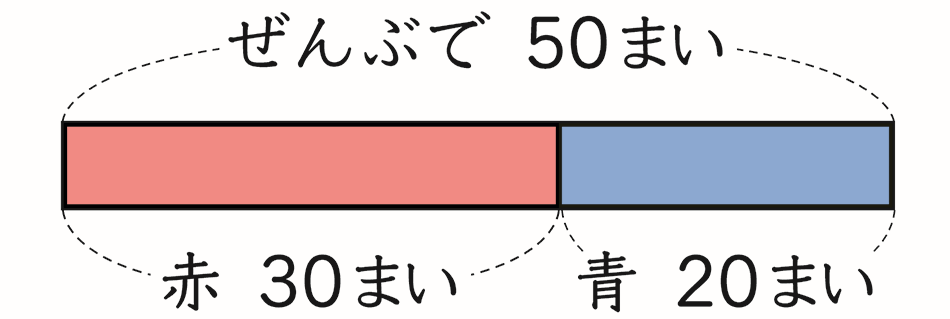
- 結論から申し上げますと、「新しい算数」では、原則として、問題文に出てくる順番に、上部から下部へと全体や部分を図に表しています。例えば、2年上巻87ページの問題１で、問題文は以下のようになっています。
「ゆきさんのクラスでは、①きのうまでにメダルを83こ作りました。②今日は、46こ作りました。メダルは、③ぜんぶで何こできましたか。」
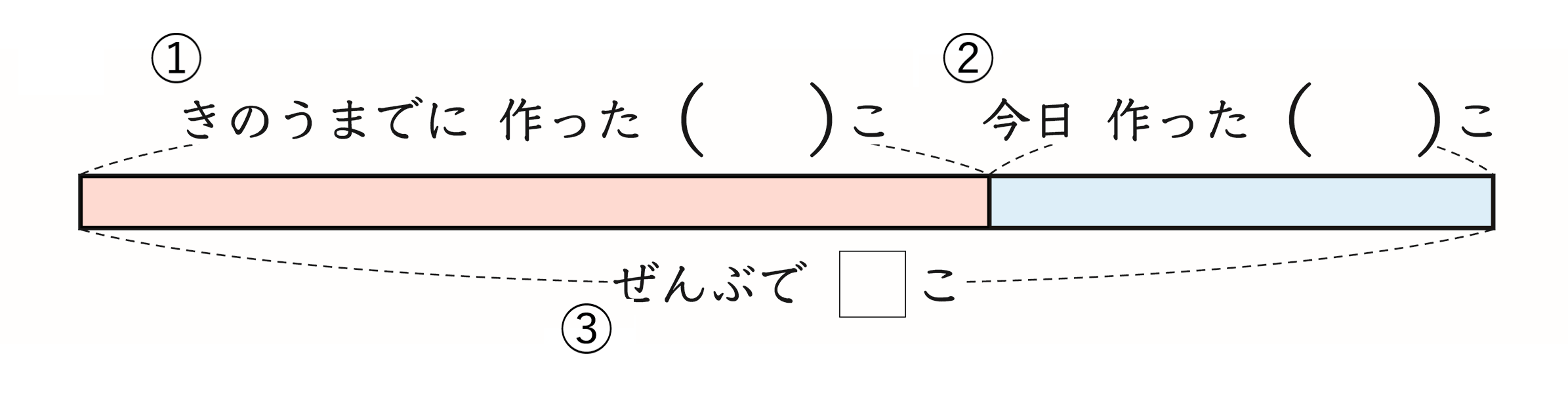
したがいまして、①～③の順番に、部分である①「きのうまでに作った数」、②「今日作った数」を上部に、全体である③「ぜんぶの数」を下部に表しています。このように、問題文に登場する順に従って図に表していくことは、児童にとって自然であり、場面の数量関係の把握が無理なくできます。特に、逆思考の場面では、同じように図に表していくことで、順思考の文脈で場面を解釈しやすくなり、全体と部分のどれを求める問題であるかが明確に分かり、演算決定も容易にできるようになります。
しかしながら、図における全体と部分の表し方について、一般に何かきまりがあるわけではありません。教科書では、上述のような考え方に基づいて問題文に出てくる順番に表すことを原則としていますが、例えば、常に全体を上部、部分を下部に表すなどしても差し支えありません。 - 九九の唱え方は教科書に掲載されている以外にも、例えば「三六（さんろく）18」「四八（しわ）32」など様々な唱え方がありますが、どの唱え方が正しいのでしょうか。
- 九九の唱え方には様々なものがあります。私どもでは、教科書を編集するにあたり、算数をご研究されている先生方を中心に広く情報を集め、最も一般的であると判断した唱え方を教科書に掲載しています。しかしながら、先述しました通り九九の唱え方には様々なものがあり、正しい唱え方というものは定められません。九九を唱える目的は正しい積を得ることですので、先生方や児童に分かりやすい唱え方でご指導いただくことが適切であると考えます。
なお、かつては各地域の唱え方を尊重し、教科書には九九に振り仮名を付けていませんでしたが、一斉唱和など学級内で統一する必要性を考慮して、現在のように振り仮名を付けるようにしています。 - （1）教科書２年上巻18ページの「35＋29」のたし算の筆算では、繰り上がった「１」は、
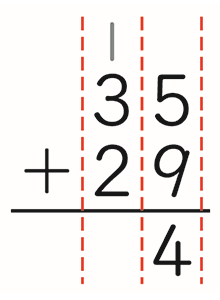
のように記述されています。このように、補助数字を書く位置は、被加数の上（上記の例で「３」の上）と決まっているのでしょうか。
（2）教科書２年上巻30ページの「47－18」のひき算の筆算では、十の位には繰り下げたことは示されていますが、一の位には繰り下げた「１」については示されておらず、
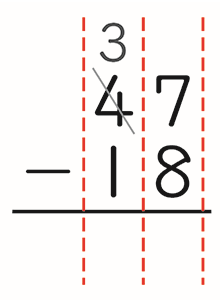
のように記述されています。繰り下がりのある場合の補助数字について、例えば上記の例で、一の位の7の上に「１」、「１０」などと書いたり、一の位の7を斜線で消して
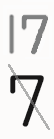
などと書いたりしてはいけないのでしょうか。
（3）教科書３年上巻112ページの「16×4」のかけ算の筆算では、
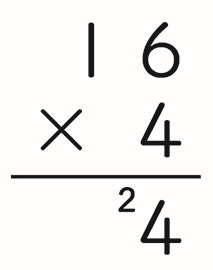
と記述されています。この場合、補助数字を書く位置は、答えの十の位の上と決まっているのでしょうか。（横棒の上に補助数字を書いてはいけないのでしょうか。） - 補助数字の書き方には様々な方法がありますが、正式なものはありません。したがいまして、教科書では、一般的に通用しているもの、計算の誤りが少ないもの、以後の学習においても適用できるものなどを判断基準とし、教科書のような表記にしました。また、以下の点なども配慮しました。
（１）たし算の筆算
・２年生の発達段階を考えると、できるだけ書きやすく、シンプルな方法が望ましいと考えます。
・繰り上がりのあるたし算の誤答の代表的な原因に、繰り上がりを忘れることがある。そのため、まずは繰り上げた「１」の処理をし、その後、位同士の計算をする習慣をつけたほうがよいと考えます。
（２）ひき算の筆算
・たし算と同様に、できるだけ書きやすく、シンプルな方法が望ましいと考えます。
・この考え方に基づけば、ひき算の筆算では、一般的に一の位の計算を最初に考えますが、繰り下がりがある場合、1繰り下げなければひけないことをまず意識することから、一の位の7の上に「１」「10」などとかいたり、一の位の7を斜線で消して「17」と書いたりする必要感は低いと考えます。
（３）かけ算の筆算
・教科書（３年上巻112ページ）では、「16×4の筆算のしかた」の枠の左側に、部分積を２段に分けて書いた筆算の準形式を例示して「筆算のしくみ」を表しています。補助数字はこの準形式との橋渡し的な役割も果たしていると考えます。
・質問にありました、補助数字を横棒の上に書くことも考えられます。しかし、３年の第17単元「かけ算の筆算(2)」で乗数が２位数以上になると、筆算形式では部分積が複数の段になるため、横棒の上に補助数字を書くことができなくなります。
なお、教科書に掲載するにあたって、補助数字の書き方自体も「厳格に指導すべき内容」として受け止めてしまうなどの誤解を避ける必要があります。補助数字の位置づけとして、あくまで、計算結果を正確に求めるための便法の１つとして取り上げていることを明確にするために、枠の外に置き、吹き出しで紹介するなど、抑えた表現方法で記しました。このように、補助数字は必ず書かなければならないものではなく、学級の実態や先生方の教材観に基づいて、柔軟に対応していただくべき内容であると考えています。 - あまりのあるわり算の答えが「14÷3＝4あまり2」と書かれていますが、「14÷3＝4･･･2」のように書いてもよいのでしょうか。
- 結論から申し上げますと、学級内などでのルールとしてならば、「あまり」を「･･･」で表記しても差し支えないと考えます。
教科書で「14÷3＝4･･･2」という表記を扱っていないのは、「･･･」は数学記号ではなく、普遍的に認められる表記といえないということが理由です。
また、「14÷3＝4･･･2」のように表記しますと、児童が等号の意味を誤解することにつながりやすいと考えられます。等号は左辺と右辺が等しいときに用いる記号ですが、児童は等号の意味を「答えを出すもの」や「式と式をつなぐもの」程度に認識していることも多いようです。そのような誤った（もしくは不十分な）認識を持ったまま「14÷3＝4･･･2」のように表記しますと、「･･･」も等号と同じような記号であるととらえたり、「･･･」を式の一部ととらえたりする誤解が生じやすくなるようです。
しかしながら、「あまり」を「･･･」と表記することは、児童にとって書きやすく、負担の軽減になります。上記のことをきちんと確認すれば、「あまり」を「･･･」と表記することは学習上大きな問題はないと考えます。 - ３年下ｐ.24の問題②（１）「１.２＋２.８」の筆算において、答え４.０の「０」のみを斜線で消し、小数点は残したままにしている理由を教えてください。
- 筆算について、正式な基準や方法が定められているわけではなく、児童の実態などに応じて柔軟にご対応いただいて差し支えないと考えています。「答えは４である」ととらえることができればよいのであり、例えば、「斜線を用いて０を消去していないから誤りである」や、「小数点を斜線で消去したから誤りである」などといったことは全く意図していません。
以下、３年下巻24ページ問題②（１）の小数の加法の筆算で、小数点以下の計算結果が「０」になる場合の、斜線を用いた消去の教科書上の表現の意図について説明します。
まず、末位の「０」について斜線で消去していることについて述べます。
筆算の手続きに従って計算すると、結果は４.０となります。ここでは、有効数字については考えませんので、４.０と４は同義であり、児童にとっても、筆算から得られた「４.０」から、「答えは４」とするのが自然です。「０」をそのまま残した場合、「小数の計算において、小数点以下が『０』になるときには、４.０と答えなければならない」との誤解が生じる可能性、また、小数点があることを忘れ、「答えは４０」という誤答が生じる可能性に配慮し、０を斜線で消去することとしました。
次に、小数点について、斜線で消去せず、そのままにしていることについて説明します。
小数点を斜線で消去することのメリットについては、例えば、
（１） 答えは４であることから「０」を斜線で消したのだから、小数点も斜線で消すことが児童にとっては自然であるということ
（２） 「答え ４.」のような誤答が生じる可能性に配慮すること
などのことが考えられます。しかし、０を斜線で消去し、答えは４であることをとらえたならば、 （２）のような誤答が生じる可能性は低いと考えます。また、（１）については、誤答や誤解が生じるというレベルのことではないことから、結果として、小数点を斜線で消去する必要性はあまり感じられないと判断しました。
以上のように、筆算には正式な基準や方法が定められているわけではありません。教科書紙面は、上述のような考え方に基づいて扱っていますが、斜線を用いた消去の表現について児童から疑問が出された場合には、その内容に応じて柔軟に対応していただくのがよいと考えます。 - 3年第18単元「三角形と角」において、導入の教材を、ストローを使った三角形づくりではなく、円周上の点を結んで三角形をつくる活動を採用している意図を教えてください。
- 主として以下のような理由からです。
・円の学習と関連づけて取り扱うこと
円と三角形の学習が引き続き平成29年学習指導要領においても同学年での取り扱いとなっているのは、両者は決して独立した内容ではなく、関連づけて取り扱うことを意図していると考えるからです。円周上の点を結んで三角形をつくる活動は、既習の円の学習を活用して学習を進めることができます。具体的には、円の中心と円周を結んだ辺の長さは、1つの円では半径の長さは等しいという円の性質から、同じ長さであることが判別できます。また、円周上の点どうしを結んだ辺の長さについては、コンパスを使って長さを比べることで「長さをはかり取る」というコンパスの機能を活用する機会にもなります。さらには、円を使うことで、向きにとらわれず自由な見方が可能になるという利点もあります。
・色覚特性への配慮
平成17年度用教科書『新編 新しい算数 4上』68ページで取り上げていた、ストローを使った三角形づくりでは、ストローの長さによって色を変えていました。そうすることで、辺の長さが視覚的にとらえやすくなります。その一方で、色覚特性によって色の判別ができない児童がいることも想定されます。
今日、教科書ではこのような色覚特性への配慮がこれまで以上に求められています。また、色の違いだけによらない表現方法も難しいため、ストローを用いた活動の掲載は見送ることにしました。
なお、円周上の点を結んで三角形をつくる活動は、ストローを用いた活動よりも準備が容易であり、児童一人ひとりが実際に活動に取り組むことができることも、この教材に変更した理由の１つです。
もちろん、ストローを使った三角形づくりは、辺の長さに着目しやすいなどの利点もあり、先に申し上げた色覚特性の問題がクリアされていれば、授業で取り扱うことは差し支えありません。 - 4年上巻15ページ「ますりんつうしん」の兆よりも大きい数で、「垓」の次が「
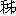（し）」となっています。書籍によっては、「じょ（のぎへんに予）」（コンピュータでは表示できませんので、以下、このように記します）となっているものもあります。どちらが正しいのですか。 - どちらの漢字が正しいかということよりも、どちらの漢字も認められて差し支えないと考えます。教科書では、次の出典の記述内容を根拠として「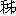」を掲載しています。「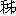」を掲載している根拠となる出典はいくつかありますが、下記の３点をご紹介します。
（１）岩波文庫「塵劫記」（1977、岩波書店）
（２）現代語「塵劫記」（2000、和算研究所）
（３）大漢和辞典〔巻八〕（大修館書店）
（１）岩波文庫「塵劫記」の14ページには、次のように記されています。
『（三）「じょ(のぎへんに予)」は中国の数学書にはすべて「のぎへんに市」（これもコンピュータでは表示できません）または「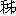」とある。「のぎへんに市」
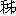・「」は同字。「じょ（のぎへんに予）」は写し誤りであろう。げんに「塵劫記」漢文序には「のぎへんに市」とある。』
（２）現代語「塵劫記」の39ページの注意書きには、次のように記されています。
『「じょ(のぎへんに予)」は正しくは「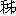」である。寛永4年版序文では「のぎへんに市」が使われているが、吉田は禾（のぎへん）の「じょ(のぎへんに予)」を用いた。吉田以外にそれまで「じょ(のぎへんに予)」を使った人はいない。』
（３）大漢和辞典〔巻八〕には、「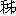」の解説に、数の単位として、垓の次にくる単位であることが記されています。また、この辞典には、「じょ(のぎへんに予)」の記載がありません。
なお、一般によく知られている「塵劫記」そのものには、「じょ(のぎへんに予)」が用いられていますので、このことなどを根拠として「じょ(のぎへんに予)」を用いている書籍もあると考えられます。
- 4年の単元配列で、「わり算の筆算（２）」の後に「概数」を配置している理由を教えてください。
- 大きくは、２つの理由があります。
（１）子どもの数感覚を大切にしたいこと。また、わり算の筆算の学習を通して、さらに数感覚を伸ばしたいこと
計算単元においては計算の仕方を確実に理解することはもとより、計算を通して子どもの数感覚をいっそう伸ばすこともねらいとすべきであると考えます。わり算の筆算の学習に際しては、先に四捨五入を指導しておき、四捨五入して仮商を立てる方が子どもにとって負担が少なく、また、便利な面もあります。しかし、その反面、四捨五入を前面に出しすぎますと、機械的な数処理に陥りがちといった面も持ち合わせていると考えます。すなわち、計算する前に答えの見積もりをしたり、数の特徴を生かした計算方法を考えたりというような、本来行うべき「数をよく見る」という活動が疎かになってしまうということです。もちろん、筆算の学習ですから、アルゴリズムに則って機械的に処理できることがよさの１つではありますが、仮商を立てる場面はアルゴリズムに入る前であり、そこではできるだけ数感覚を生かすことが望ましいと考えます。
そして、「わり算の筆算(２)」においては、除数の25を子どものもつ数感覚により20とみたり30とみたりしながら計算するなど、子どもの数感覚を活かしながら学習を進めていく展開を採用しています。
（２）「概数」先習の単元配列の弊害が生じたこと
以前に、「新しい算数」においても「概数」→「わり算の筆算(２)」という配列を試みたことがあります。その際の意図は、「仮商を立てる際の方法の１つとして四捨五入の活用も考えられる」というものでした。しかし、結果として「四捨五入の理解が不十分な子どもは『わり算の筆算(２)』の学習がますます困難になる」というご指摘や、「四捨五入を学習した後では、25を20とみることに戸惑う子どもも少なくない」というご報告も多数いただきました。また、先に四捨五入を扱った後では「数感覚を自由に活用して仮商を立てる学習が成立しづらい」というご指摘をいただいたことも付け加えておきます。
以上のような理由から、「わり算の筆算（２）」の後に「概数」を配置しています。
なお、実態などによっては、「概数」を先に指導するという可能性も考えられます。指導順序の入れ替えやすさに配慮して、「わり算の筆算（２）」と「概数」を近づけた単元配列としています（上巻、第6単元と第7単元）。
- 4年「がい数の表し方と使い方」の問題で、概数を答えるとき、概数の前に「約」をつけなければいけないのでしょうか。
- 4年「がい数の表し方と使い方」の単元では、答えが概数であるかが明確になっていない場合は、答えに「約」をつける必要性が高いと考えますが、「新しい算数」4上ｐ.122△2、ｐ.124△3のように、問題文に「がい数にしましょう」とあり、概数で答えることが明確な場合は、答えに「約」をつけていません。それは、概数で答える数に必ず「約」をつけますと、概数を答える問題では必ず「約」をつけなければいけないという誤解や、「約」がついていない数は概数でないという誤解を生む恐れがあるからです。
一部例外として、「新しい算数」4上ｐ.121△1は、初めて概数を学習する場面であるため、四捨五入して処理した数が概数であることを明確に意識づけるために、答えに「約」をつけています。
日常で目にする道路標識、案内板などの「〇〇 5km」などといった表示は概数ですが、一般に、「約」はついていません。また、2、3年の長さ、かさ、重さの学習で計器の目盛りを読むときに、目盛りと目盛りの間の数について目盛りの近い方で読んで数量を表します。すなわち、測定値は概数ですが、「約」や「およそ」をつけないで表してきています。このように、日常場面、既習場面で概数と出合ったり使ったりしてきていますが、「約」をつけないで表すことが多々あります。
これらのことから、概数であることが明確な場合には、「約」をつけなくても差し支えないと考えます。
ただし、教師用指導書の答えに「約」がついていないところで、「約」をつけても誤りではありません。指導者の裁量で柔軟に取り扱うべきことと考えます。 - 概数の学習で「上から◯けたのがい数にしましょう。」という発問が教科書にあります。この発問の「上から」は、「うえから」「かみから」のどちらの読み方をすればよいのでしょうか。
- 「うえから」と読んでも「かみから」と読んでも差し支えありません。同様に、「下から◯けた」について、「したから」と読んでも「しもから」と読んでも差し支えありません。児童にとって意味を理解しやすい読み方でご指導されることが肝要かと考えます。
- 5年「四角形と三角形の面積」で、平行四辺形から導入する理由を教えてください。
- 大きくは、３つの理由があります。
（１）平行四辺形は既習の長方形に等積変形しやすいこと
平行四辺形は、分解し、部分の三角形や台形を移動させることにより、既習の長方形に変形しやすい図形です。三角形の場合、直角三角形を除き、面積を求めるには、頂点からの垂線によって２つの直角三角形に分割して、それぞれの直角三角形の面積を求める手順を踏むことになります。これらの手続きは、平行四辺形の場合に比べ、操作が煩雑である上、式変形も単純ではありません。
（２）三角形の面積公式が導きやすいこと
（１）と少し重複しますが、三角形から入りますと平行四辺形の面積公式を導く際も、手続きが煩雑になることが考えられます。三角形の面積公式を利用する考えでは、三角形の面積（底辺×高さ÷２）を再度２倍することになり、低位の子どもには２で割ったものを２倍することは混乱の要因にもなりかねません。平行四辺形から入りますと、三角形の面積＝平行四辺形の面積÷２であることから、三角形の面積公式が導きやすいと考えます。
（３）多様な考えが出やすく、子ども自身が既習を活用しやすいこと
このことがいちばん大きい理由と考えます。平行四辺形を先行させる順序ですと、平行四辺形の後に、三角形やその他の図形の面積の求め方を学習することになりますが、三角形や台形などで既習の図形に帰着して考える際、いろいろな選択肢が生まれます。また、その方法も多様です。
一方、三角形から入る場合には、常に三角形に戻って考えればよいという考え方が基本になります。これは三角形から入ることの長所とも言えます。確かに基本図形はすべて三角形に分割することができますので、三角形を基本に考えて図形の面積を求められるという数学的な魅力があります。
また、この単元ではただ図形の面積の求め方を学習するだけでよいのかどうかを考えたとき、この単元は、数学的な見方・考え方を働かせながら算数における学び方を学ぶ場面として、既習を用いて多様な考えによって解決できること、一見異なる多様な考えが最終的に１つの式にまとめて表されることなど、主体的・対話的で深い学びを実現するのに最適な内容と位置づけることもできると考えます。
平行四辺形と三角形、どちらの求積から導入する場合でも、既習を活かすこと、児童の多様な考えを取り上げること、解決方法の検討を通して１つの式（公式）にまとめられることなどをおさえて学習を進めていただくことが肝要かと考えます。